Mathematik

Mathematik Q1

Übungsaufgabe

Da ich am Dienstag nicht anwesen sein kann, ist hier die Übungsaufgabe. Viel Spaß!!!

Die natürliche Exponentialfunktion und ihre Ableitung

In der folgenden Grafik sehen Sie den Graphen der Funktion f und den Graph der Ableitungsfunktion f' von f eingezeichnet. Wenn man sich die Graphen genauer anschaut, erkennt man, dass sie jeweils proportional zueinander sind, sich also nur um einen Faktor unterscheiden. Für genau einen Wert von a gilt nun f(x) = f'(x).

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Die Ableitung der Exponentialfunktion Um die Ableitung einer neuen Funktionsklasse zu bestimmen, muss man immer wieder auf die grundlegende Definition zurückgreifen. Sei beispielsweise a=4. Dann ergibt sich aus dem Differenzenquotienten: 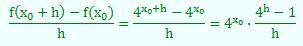Die Ableitung einer Funktion ist nach Definition der Grenzwert des Differenzenquotienten. Also ergibt sich für unser Beispiel: 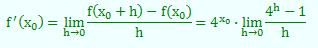Der Proportionalitätsfaktor ist also durch den letzten Grenzwert gegeben. Setzt man nun kleine Zahlen für h ein, so erhält man einen Faktor der ca. 1,3863 beträgt.

Kommen wir wieder zur obigen Beobachtung zurück! Wir suchen also eine Zahl, für die gilt: f(x)=f'(x).
in unserer Betrachtung heißt das jetzt, dass der Proportionalitätsfaktor, der durch den Grenzwert angegeben ist den Wert 1 haben muss. Diese Zahl definieren wir uns als e. Aber wie groß ist e???
Dazu schauen wir uns den Grenzwert noch einmal genauer an:

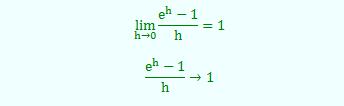
Ersetzt man in dieser Formel noch h durch 1/n, so gilt weiterhin:

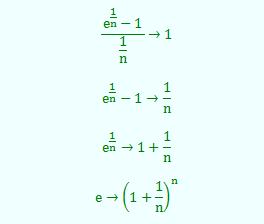
Setzt man für n beispielsweise 10 000 ein, so ergibt sich ein Wert e ≈ 2,71815.

Definition: Die Euler'sche Zahl e ist genau die Zahl, für die die Exponentialfunktion f(x)=e^x mit ihrer Ableitungsfunktion f' übereinstimmt. Man nennt dann die Exponentialfunktion zur Basis e auch natürliche Exponentialfunktion. Es gilt e≈2,7182818...